「速度，加速度，落下運動」　例題２

2005.11.10 解説：高瀬寿乃
出題：中村陽一
教育センター ＞ SEC Video Library ＞ One-point アドバイス（物理）
解説ビデオ

例題２

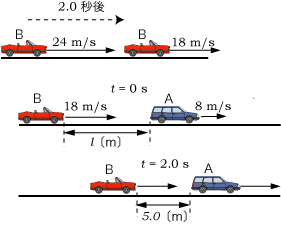
霧の高速道路を速さ 24〔m/s〕で走っていた自動車Bの運転手が，前方に低速の自動車Aを発見し，一定の加速度で減速し始めて，2.0〔s〕後に速さ 18〔m/s〕になった。 この瞬間を t = 0〔s〕とする。一方，速さ 8.0〔m/s〕で進んでいたAは t = 0〔s〕の時から一定の速度で加速し始めた。 その結果， t = 2.0〔s〕のとき，車間距離はもっとも短くなって 5.0〔m〕となったが，衝突を免れた。 A，Bの進行方向を正とする。
  1. まずBの加速度 aB を，次にAの加速度 aA を求めよ。
  2. t = 0〔s〕の瞬間の車間距離はいくらか。

解答・解説

最初はBの方が速いので車間距離はどんどん縮まってゆくが，Bが減速しAが加速するため，ある時点で速度の大小関係が逆転し，Aの方が速くなるため車間距離は広がってゆく。 従って､BとAの速度が等しくなったとき車間距離が最短となっている。

（１）の解答例

まずBの加速度を求める。 自動車Bは 2〔s〕間に 24〔m/s〕から 18〔m/s〕に減速したのだから，この間の加速度は

　〔m/s2〕

と求められる。車間距離が最短となった t = 2.0〔s〕のとき，それぞれの速度が等しくなるので t = 0〔s〕での BとAの初速度をそれぞれ vB0 = 18〔m/s〕，vA0 = 8.0〔m/s〕とすると，2.0〔s〕後のそれぞれの速度は

　〔m/s〕および
　〔m/s〕となり

vB = vA より aA = 2.0〔m/s2〕を得る。

（２）の解答例

t = 0〔0〕の瞬間のBの先端位置Oを原点とし，そのときのBとAとの車間距離を l〔m〕とすると， もっとも接近した t = 2.0〔s〕のときのAとBとの座標は

　〔m〕
　〔m〕

となる。このとき，AはBよりも5.0〔m〕前にいるので

　〔m〕

これより l = 15〔m〕となる。
教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved.