「速度，加速度，落下運動」　例題１

2005.11.10 解説：高瀬寿乃
出題：中村陽一
教育センター ＞ SEC Video Library ＞ One-point アドバイス（物理）
解説ビデオ

例題１

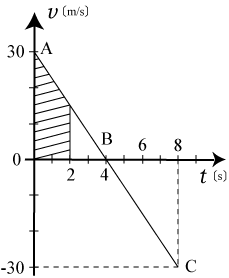
右のグラフは時刻０の時 x 軸の原点を出発し，x 軸上を運動する物体の，速度と時間の関係を表したものである（ グラフ）。 右の向きを正として，以下の問いに答えよ。
  1. 時刻 t = 2〔s〕，t = 4〔s〕，t = 6〔s〕，における物体の速度と加速度をそれぞれ求めよ。
  2. 図の斜線部の面積は何を表しているか。また，それはいくらか。
  3. 物体が原点から右へもっとも遠ざかるのはいつか。また，そのとき，物体は原点からいくら離れているか。
  4. 時刻 t = 8〔s〕における物体の位置を求めよ。

解答・解説

まず，グラフの見方だが，t = 0〔s〕で速度３０〔m/s〕（初速度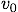 = 30〔m/s〕）で物体は右向きに進んでいる。 時間がたつにつれて速度は小さく，すなわち減速してゆき，t = 4〔s〕で速度 0 となり（一瞬停止），その後､負の速度，すなわち左向きに徐々に 速度を上げてゆく（方向転換），といった運動が示されている。このような減速運動も「負の加速度による加速度運動」と呼ぶ。
グラフの傾きが加速度を表すが，この図では傾き一定の直線となっているので， 等加速度運動である。

（１）の解答例

まず，直線の傾きから加速度を求める。この運動では加速度は一定なので，各時刻における加速度はすべて平均の加速度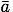 に 等しくなる。平均の加速度を求めるのに，この直線の両端の速度を使おう。グラフより t = 0〔s〕で 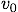= 30〔m/s〕，t = 8〔s〕で 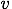= -30〔m/s〕なので､

　〔m/s2〕

と求められる。等加速度運動の速度は

　〔m/s〕

で与えられるので，t = 2, 4, 6 〔s〕における速度はそれぞれ 15, 0, -15〔m/s〕，また加速度は一定で -7.5〔m/s2〕となる。

（２）の解答例

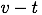グラフの面積は物体の進んだ距離を表している。従って図の斜線部は 時刻 0〔s〕から 2〔s〕までに物体が進んだ距離である。等加速度運動での進行距離は

　〔m〕

となる。別解として，台形の面積＝（上底＋下底）×高さ／２を使うと，〔m〕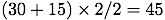となり同じ結果を得る。

（３）の解答例

図より時刻 t = 4〔s〕以降はグラフの面積が負となっていることがわかるが，これは 4〔s〕を境に物体の運動方向が反転したことを表している。つまり もときた道を戻っているのである。従って右向きの距離が最大になるのは t = 4〔s〕のときである。この時の距離は

　〔m〕

となる。別解として，三角形の面積＝底辺×高さ／２をつかうと，〔m〕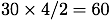となり同じ結果を得る。

（４）の解答例

8〔s〕後の移動距離は，

　〔m〕

となる。つまり最初の位置までもどってきたことになる。
教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved.