「 ２次方程式 」

出題： 摂南大学数物系教室(現:基礎理工学機構)
学習支援センター ＞ ASC Video Library ＞ One-point アドバイス（数学）
２次方程式　ax 2 + bx + c ( a ≠ 0, b, c は定数）の解は，

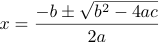
ただし判別式　 　の時は実数解なし

２次方程式の解き方

（１） 因数分解による方法

例 　i)　x ２ + 2ｘ ｰ9 = 0，　 ii)　2x 2 + 3x + 1 = 0
　
解 　i) 左辺を因数分解して ( x−3 ) ( x + 1 ) = 0 となるので　x = 3, ｰ1．
　　ii) 左辺を因数分解して ( 2x + 1) ( x + 1 ) = 0 となるので　x = ｰ1,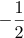
（２） 平方完成による方法
例 　ｘ ２ + 2ｘ ｰ9 = 0
　
解 　左辺を平方完成して ( x + 1 ) ２ ｰ10 = 0 となるので ( x + 1 ) ２ = 10，
両辺の平方根をとって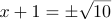　 　すなわち　
（３） 解の公式による方法
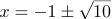
（２）の方程式　ｘ ２ + 2ｘ ｰ9 = 0　を解の公式に当てはめると

　
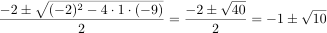
注意 　根号の中が負になるときは方程式の実数解はありません．
例 ｘ 2 + 2ｘ + 3 = 0
解 判別式 D = 2 2 ｰ4 ・2 ・ 3 = ｰ20 < 0 より解なし．

解の判別
解の公式の根号の中の式　D = b ２ ｰ 4ac　を 判別式 といいます．

i)　D < 0 　のとき，解なし
ii)　D > 0 のとき，相異なる2実数が解
iii)　D = 0 のとき ，１つの解（重解）
　
例題 　k を定数とするとき，２次方程式　x ２ + 2 ( k + 1 ) x + k ２ +2 = 0 の実数解の個数を調べなさい．
解　 判別式は D = { 2( k + 1 ) } ２ ｰ4 ( k ２ + 2 ) = 4 ( 2k ｰ1 ).
　
従って　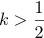 　のとき 2 個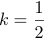， 　のとき 1 個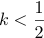， 　のとき 0 個．
スケジュールへ戻る
摂南大学 学習支援センター オリジナル教育ビデオライブラリ
学習支援センター ホーム Copyright (C) 2004-2014 Academic Support Center, Setsunan University, All Rights Reserved.
w3sec@atf.setsunan.ac.jp, TEL: 072-839-9357 学内 374, FAX: 072-813-1180
摂南大学 学習支援センター サイト内検索 　
powerd by apache