「速さと速度」
2005.11.18 教育センター 平田 慈（めぐみ）
教育センター ＞ SEC Video Library ＞ One-point アドバイス（物理）
（１）平均の速さと瞬間の速さ
移動する物体の速さが刻一刻と変化しているとき， 物体の移動した距離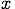
を，
その移動に要した時間 t で割った量を平均の速さという。
（ velocity に由来。単位は 〔m/s〕，〔cm/s〕，〔km/h〕など。）
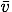は、”ヴイ バー”と読む。バーをつけることで平均値であることを表す。
ある瞬間の速さを知るには，その間の速さの変化が無視できるような非常に短い時間 Δt に
物体の移動した距離 Δ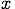 を，Δt で割って求める。
これを瞬間の速さという。
（ 単位は 〔m/s〕，〔cm/s〕，〔km/h〕など。）
Δ（大文字の”デルタ”）はギリシャ文字で、これを文字の前につけることで，その文字の表す量の非常に小さい（または短い）変化量を表す。
（２）等速直線運動とそのグラフ
一直線上を一定の速さで進む運動を等速直線運動と呼ぶ。 等速直線運動をする物体の移動距離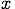 は，
速さ v とその移動に要した時間 t との積で表される。
〔m〕
このとき，移動距離 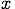と
移動時間 t は比例しているので，横軸に t をとり，
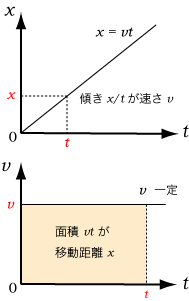
縦軸に 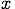をプロットすると，
直線のグラフとなる。この x ー t グラフの傾きが速さとなる。
等速直線運動では，横軸に移動時間 t，縦軸に速さ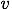 
をとると，
速さが時間によらず一定なので水平なグラフとなる。
この v ー t グラフの面積
（速さ 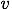× 移動時間 t ）が
t 秒間に移動した距離 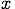を表している。
（３）速度
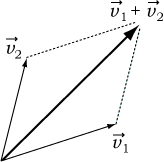
速さ 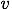に，運動の向きをあわせたものを速度といい，
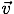で表す。矢印は，ベクトル量（大きさと方向を持つ量）であることを示している。矢印をつける代わりに太字で表すこともある。
直線運動の場合，速度の向きを正負の符号で表す。（向きが反対になれば符号が逆になる。）
（４）速度の合成
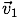速度 
に速度 
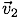の合成速度 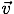は，
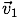と 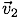を隣り合う二辺とする平行四辺形の対角線で表せる。
（５）相対速度
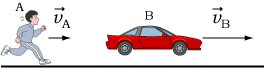「相対的」とは､お互いの状況によって変わってくるというような意味である。
二つの物体間の速度（片方からもう片方を見たときの速度）もそれぞれの物体の状況に応じて変わってくるので，「相対的」であるといえる。
たとえば，速度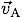 
で動いている人Aから，
速度 
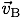で動いている物体Bを見たときの
相対速度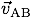 
は，
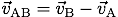となる。
ならAから見てBは遠ざかってゆき，
ならAから見てBは近づいてくる。
ならAから見てBは止まって見える。
教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |