「ベクトル 内積・外積 その物理学的イメージ」2004.7.24 摂南大学 工学部 電気電子工学科 井上雅彦
工学部 教育センター ＞ SEC Video Library ＞ One-point アドバイス（物理）
物理学で扱う物理量には，大きさだけを持つスカラーと，大きさの他に方向をもつベクトルがある。
これらの物理量の積が別の物理量となる場合について考えよう。
まず，スカラー同士の積だが，どちらももともと方向を持っていないので
これはあきらかにスカラーとなる。
次にスカラーとベクトルの積はベクトルとなる。方向はもとのベクトルと同じで，その大きさがスカラー倍される。
最後にベクトル同士の積であるが，この積の結果はスカラーとベクトルの二つのケースが考えられる。これらはそれぞれ内積（スカラー積）および
外積（ベクトル積）と呼ばれる。
内積（スカラー積）
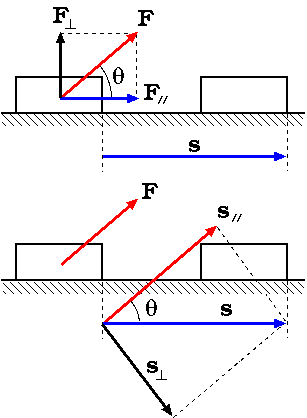
図のように床の上にある物体に力F〔N〕を加え s〔m〕移動させたときの仕事 W〔J〕について考えてみよう。まず s の方向を基本として，力 F を s に垂直な成分 F⊥ と s に平行な成分 F// に分けて考えると，この場合物体の移動に関係したのは F// だけなのでなされた仕事はとなる。Wには方向性はなく（移動方向が東だろうが西だろうが疲れ方は同じ）スカラー量となる。〔J〕
逆に F の方向を基本として，移動距離のベクトル s をF に垂直な成分 s⊥ と水平な成分 s// にわけて考えると， 加えられた力の方向に移動した距離は s// なのでなされた仕事は
となり先ほどの結果と一致する。これらはまとめてベクトルの内積で表現することができる。〔J〕
つまり，物理学で内積を使用する場合は，二つのベクトル量の同一方向成分（平行成分）の積を求めていることになる。 おなじ方向の成分の積ということで，演算の結果，方向に関する情報は無くなってしまう。〔J〕
外積（ベクトル積）
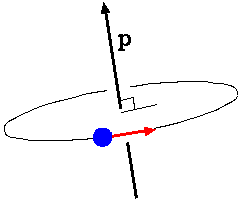
外積の話題に入る前に回転運動（回転力）の表現について整理しておこう。回転には回転軸があるので，この軸の方向で回転の方向性を表現する。 なお，ひとつの軸には二つの方向が考えられるが，回転に対して右ねじの進む向きと定義する。また，回転の度合い（運動量とか，力とか） をこのベクトルの大きさで表すことにすると，回転は図の p ベクトルのように一つのベクトル量として表現できる。
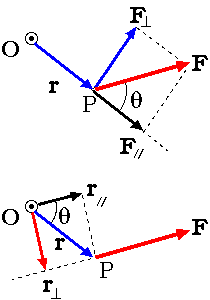さて，紙面上に O 点と P 点があり，紙面に平行な力 F〔N〕を P 点に加えた場合の O 点のまわりの
力のモーメント M〔Nm〕について考えてみる。まず，P 点の位置ベクトル r の
方向を基準にして，力 F を r に平行な成分 F// と垂直な成分 F⊥に分けて考える。
明らかに F// は回転に寄与しない。
従って力のモーメントの大きさは，
またベクトル M の方向は回転の右ねじ進行方向なので，紙面に垂直で上向きとなる。〔Nm〕
逆に力 F の方向を基準として，位置ベクトル r を F に 平行な成分 r// と垂直な成分 r⊥ に分けると， 明らかに r// は回転に寄与しない。従って力のモーメントの大きさは，
となり，先ほどの結果と一致する。またベクトル M の方向は回転の右ねじ進行方向なので，紙面に垂直で上向きとなる。 これらは方向も含めてまとめてベクトルの外積で表現できる。〔Nm〕
つまり物理学で外積を使用する場合は，二つのベクトル量の直交する成分（垂直成分）の積を求めていることになる。演算結果は回転に対応するためやはりベクトル量となり， その方向は回転の右ねじ進行方向となる。外積では演算順序を変えると符号が逆になるので注意を要する。 これは回転方向が逆向きになることに対応している。〔Nm〕
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |