「ラジアン,ステラジアン」2004.7.14 摂南大学 工学部 電気電子工学科 井上雅彦
工学部 教育センター > SEC Video Library > One-point アドバイス(物理)
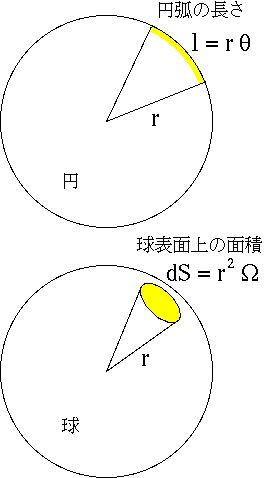 円の中心から2本の直線を図のように引くと扇形ができる。扇形は円周の一部(黄色の部分)を切り取ることになるが,その部分を円弧という。
円弧の長さは扇形の中心の角度に比例する。そこで円弧の長さで角度を表すことが考えられる。
円の中心から2本の直線を図のように引くと扇形ができる。扇形は円周の一部(黄色の部分)を切り取ることになるが,その部分を円弧という。
円弧の長さは扇形の中心の角度に比例する。そこで円弧の長さで角度を表すことが考えられる。
同じ角度でも円弧の長さは円の半径によって
変わってくるので,半径 r = 1 の円(単位円)の円弧の長さで角度を表すことにする。この方法を弧度法という。単位は〔rad〕(ラジアン)である。
扇形の中心角が 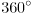 の場合,円弧の長さは円周と一致するので,
の場合,円弧の長さは円周と一致するので,
となるが,単位円では r = 1 なので〔m〕
即ち 360度は 2π〔rad〕となる。また,円周の長さが半径 r に比例することからわかるように円弧の長さは半径 r に比例する。 従って角度 θ〔rad〕の扇形において,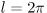
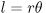 〔m〕
〔m〕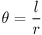 〔rad〕
〔rad〕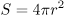 〔m2〕
〔m2〕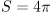
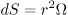 〔m2〕
〔m2〕
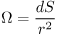 〔sr〕
〔sr〕