「レーザポインタでミクロの世界を測定する」2004.7.17 摂南大学 工学部 電気電子工学科 井上雅彦
レーザポインタから出るレーザ光は単一波長で進行方向も一方向（平面波），また位相がそろっているため
干渉しやすい光となっている。ここでは波長 λ = 532 [nm] の緑色レーザポインタを使用する。もちろん一般に市販されている
赤色レーザポインタを使っても同様の実験が可能なので，持っている人はぜひ一度お試しいただきたい。
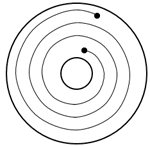
測定対象は CD（コンパクトディスク）である。CD の 記録面には図のように香取線香のように一筆書きでデータが記録されている。これを トラックと呼ぶ。断面を見ると，このトラックの部分が少し出っ張った形になっている。実際にはこのトラックは途切れ途切れになっていて それがデジタルデータに対応しているのであるが，ここではそのトラックの途切れは無視する。トラックの間隔は 1.6〔μm〕と定められている。 このトラック間隔を測定してみよう。
CD を水平な台の上において斜め上方からレーザ光をあてると２つの回折スポット（斑点）が観測された。
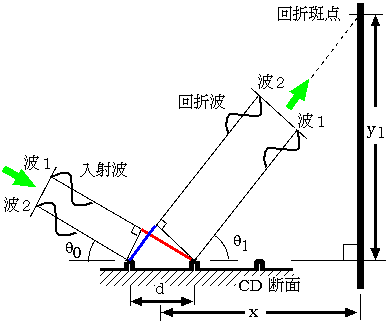
この回折スポットが生じる条件について考えてみる。図のようにレーザポインターからの波１と波２が入射角θ0 で
CD に入射し，それぞれトラックで散乱して角度θ1の方向に回折スポットが生じたとする。
これらの波がトラックに到着するまでの進行距離の差は図の赤い直線部分で d cosθ0 またトラックで散乱して壁に
到着するまでの進行距離の差は図の青い直線部分で d cosθ1 である。従ってレーザポインタを出てから壁に到着するまでの
進行距離の差（光路差）は d cosθ1 - d cosθ0 で，これが波長の整数倍になっている。
ここで m は整数である。（１）
注：もっとも明るい回折スポットは入射角と反射角が等しく光路差は０，即ち m = 0 とすぐにわかる。 この回折波は入射波に対して反射の法則を満たしている。もう一つの回折スポットについても同様に考えれば良い。ただし，となりあった回折スポットの 整数 m は１だけずれるので，
と表すことができる。（２）式から（１）式を引くと，（２）
入射角θ0に関する項や m はキャンセルアウトされる。つまりこれらの値は測定する必要がない。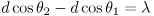
レーザ波長λはあらかじめ 532〔nm〕であることがわかっているので，角度 θ1 と θ2 がわかればトラック間隔 d を計算することができる。 角度は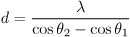
のように求められるので，実験では距離 x, y1, y2 を測定すれば良い。教育センターで 実測した結果を表にまとめる。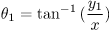
| x〔cm〕 | y1〔cm〕 | y2〔cm〕 |
| | | |
このように波の回折現象を利用すると目に見えないような小さな距離を測定することができる。結晶中の原子の間隔（0.1〜1〔nm〕のオーダー） もＸ線や電子の波の回折を利用して測定されている。
この実験は身近なもので簡単にできるので，興味を持った人はぜひ一度試してみてください。なお，赤いレーザ光の波長は 650〔nm〕のものが 多いようですので，波長が記載されていない場合はこの値を使ってみてください。 またはトラック間隔 1.6〔μm〕を既知として，逆にレーザ光の波長を決定するのも面白いと思います。
レーザ光を直接見ないように注意してください！
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |