「運動量と力積」
2004.7.28 教育センター 平田慈
教育センター > SEC Video Library > One-point アドバイス(物理)
キャッチボールをしているとき,ボールの速度が大きい程,また,ボールの質量が大きい程 ボールを受け取る手が感じる衝撃は大きい。つまり,ボールの運動の激しさは,運動している ボールの質量と速度に関係していると考えられる。そこで質量 m〔kg〕の物体が速度 v〔m/s〕で運動しているときに, この物体の運動の激しさを表す量として質量と速度の積 mv を考え,これを運動量 P と呼ぶ。
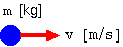
次に物体の運動量の変化について考えてみよう。〔kg・m/s〕
*運動量は速度と同じ向きを持つベクトルである。
一直線上を速度 v〔m/s〕で動いている質量 m〔kg〕の台車に,運動と同じ向きに一定の力 F〔N〕を 時間 Δt〔s〕間加えた。力を加えた後の台車の速度を v'〔m/s〕とすると,加速度 a〔m/s2〕は
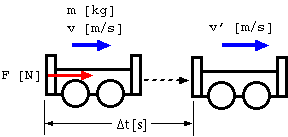
となり,これを運動方程式 ma = F に代入すると,〔m/s2〕
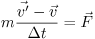
(1)
 が得られる。(1) 式はニュートンが運動の法則として示したもので,
が得られる。(1) 式はニュートンが運動の法則として示したもので,「運動量の時間的変化の割合は,物体に働いた力に等しい」ということを示している。 さらに,(1) 式の Δt を右辺に移項して得られる式
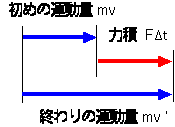
より,運動量の変化は力 F〔N〕だけで決まるのではなく,力 F〔N〕のはたらいた時間 Δt〔s〕に比例する ことがわかる。このような力 F〔N〕と力が働いていた時間 Δt〔s〕との積 FΔt を力積という。(2)
つまり (2) 式は「物体の運動量の変化は,その変化の間に物体が受けた力積に等しい」ことを示している。〔Ns〕
*力積は力と同じ向きをもつベクトルである。
運動量 mv〔kg・m/s〕と力積 FΔt〔Ns〕は,単に質量と速度,力と力が働いた時間の積としてとらえるのではなく, 積そのものが一つの物理量であることを理解して欲しい。
教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |