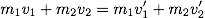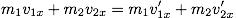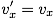「運動量保存の法則」
2006.1.31 教育センター 平田 慈(めぐみ)
教育センター > SEC Video Library > One-point アドバイス(物理)
(1)運動量
運動量:物体の運動の激しさを表す量。〔質量〕×〔速度〕〔kg・m/s〕
(2)力積と運動量の変化
質量 m の物体に F の力が時間 t だけ作用した後,その速度が v から v' に変化したとすれば,物体に働く力 F と,その力が働いている時間 t の積 Ft をこの時間内に物体に与えられた力積と言う。 上式は「物体の運動量の変化は,その物体に与えられた力積に等しい」ことを表している。∴
〔N・s〕
(3)運動量保存の法則
(1) 直線上の衝突
外から力が加わらない限り,衝突の前後で各物体のもつ運動量は変化するが,運動量の総和は変化しない。(2) 平面上の衝突
運動方向の異なる2つの物体の衝突も,各運動量を x 方向と y 方向に分解して考えると,それぞれの方向において運動量の成分の和は変化しない。x 成分:
y成分: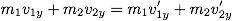
(4)反発係数(はねかえり係数)
(1) 物体と物体が衝突する場合
一直線上を v1,v2 で運動する A,B 二つの球が,衝突後 v1',v2' に変化したと すると,衝突前後の2球の相対速度の比 e は,2球の種類によって一定であり,これを反発係数と言う。衝突前後の相対速度の向きは反対方向となるので,マイナス符号をつけることで e は正の数値となる。 e は 0 〜 1 の値をとり,e = 1.0 のとき完全弾性衝突,e = 0 のとき 完全非弾性衝突という。一直線上で2球が衝突する場合には運動量保存則が成り立つので, 反発係数の式と運動量保存則を用いてうんどうを解析することができる。:一定
(2) 壁や床ではねかえる場合
小球と壁や床との衝突の場合,壁や床は質量が非常に大きいだけでなく,他のものに拘束されている場合が多いので, 衝突のときに作用する力は内力のみではない。 従って運動量保存則は成立せず,反発係数の式のみで解くことになる。平面に垂直な衝突では,小球の衝突前後の速さを,v,v' とすると
なめらかな平面と斜めに衝突する場合には,衝突前の速度の,面に平行な成分を vx,面に垂直な成分を vy , また衝突後の速度の,面に平行な成分を vx',面に垂直な成分を vy' とすると, 面はなめらかなので面に平行な速度成分は変化せず,垂直な速度成分は反発係数倍されることになる。 従って以下のようになる。&there4
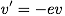
面に平行な速度成分:
面に垂直な速度成分: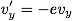
教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |