「力学的エネルギー保存の法則」　例題２

2006.2.2 解説：教育センター　平田　慈
出題：中村陽一
教育センター ＞ SEC Video Library ＞ One-point アドバイス（物理）
解説ビデオ

例題２

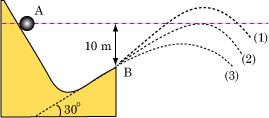
図のようになめらかな斜面上の点 A に置かれた質量 2.0〔kg〕の球が，初速度 0 ですべりだした。 重力の加速度 g を 9.8〔m/s2〕として次の問に答えよ。
（１）AB間の落差を 10〔m〕とすると，B 点での球の速さは何〔m/s〕か。
（２）B 点では水平と 30 ° の角をなす方向へ飛び出した。飛び出したあとの球の軌跡はどうなるか。 図の (1) 〜 (3) から正しいものを選べ。
（３）B 点での速度の水平成分，鉛直成分はそれぞれ何〔m/s〕か。
（４）最高点に達したとき，球の持つ運動エネルギーは何〔J〕か。
（５）最高点の高さは B 点から何〔m〕のところか。

解答・解説

（１）の解答例

A，B 間の位置エネルギーの差が B 点における運動エネルギーに変化したわけだから， B 点での速度を v とすると，
2.0 × 9.8 × 10 = ( 1 / 2 ) × 2.0 × v2
∴ v = 14〔m/s〕
答 14〔m/s〕

（２）の解答例

最高点に達したとき，水平方向にある速さで運動しているので，この運動エネルギーの分だけ， 位置エネルギーは A 点での位置エネルギーよりも小さくなっている。つまり最高点は A 点よりも低くなる。
答　(3)

（３）の解答例

（１）で求めた速度を水平成分と鉛直成分に分ける。
水平成分：14 cos 30 ° = 12.1〔m/s〕，鉛直成分：14 sin 30 ° = 7.0〔m/s〕
答　水平成分 12.1〔m/s〕，鉛直成分 7.0〔m/s〕

（４）の解答例

飛び出したあと，球の水平方向の速度は変化しない。従って最高点での速度は（３）で求めた水平成分の速度と等しいので 運動のエネルギー K は，
K = ( 1 / 2 ) × 2.0 × ( 14 cos 30 ° )2 = ( 1 / 2 ) × 2.0 × ( 7 √3 )2 = 147〔J〕
答　1.5 × 102〔J〕

教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved.