「関数のグラフの平行移動」
2004.7.28 教育センター 小林俊公
工学部 教育センター > SEC Video Library > One-point アドバイス(数学)
関数のグラフの平行移動を考えてみます。
基本となるのは、平面上の点の平行移動です。
1. 点の平行移動
xy-平面上の点 P (x, y) を x 軸方向に p,y 軸方向に q だけ平行移動した 点を Q (X, Y)とします。 このとき、X, Y は(*)のように表されます。 逆に、 P は Q を x 軸方向に - p、y 軸方向に - q だけ平行移動した 点と見ることができますから、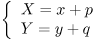
(**)のように表すことが出来ます (**)は(*)の書き換えです)。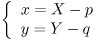
このことをふまえて、グラフの平行移動を調べてみます。
2. グラフの平行移動
y = f (x) のグラフを x 軸方向に p,y 軸方向に q だけ平行移動したグラフを 表す方程式を求めます。平行移動したグラフ上の点 P (x, y) を x 軸方向に - p、y 軸方向に - q だけ平行移動 した点を Q とすると、Q は元の y = f (x) のグラフ上にあります。 そして、Q の座標は、Q (x - p, y - q) と表されますから、
が成り立ちます。 これが、y = f (x)を平行移動したグラフを表す方程式となります。, すなわち,
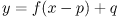
具体的な例をみてみます。
3. 二次関数の例
という二次関数を考えてみます。 この方程式は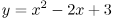
のように変形できます。これは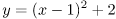
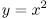 という放物線を表す関数の方程式とよく似ています。
という放物線を表す関数の方程式とよく似ています。
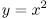 において、x を x - 1 に、y を y - 2 に置き換えますと
において、x を x - 1 に、y を y - 2 に置き換えますと
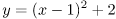 になります。
ですから、
になります。
ですから、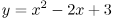 のグラフは、
放物線
のグラフは、
放物線 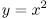 のグラフを
x 軸方向に 1,y 軸方向に 2 だけ平行移動した、放物線になります。
のグラフを
x 軸方向に 1,y 軸方向に 2 だけ平行移動した、放物線になります。
実際にグラフを書くときには、放物線の特徴の一つである、頂点に注目してみましょう。
頂点も同じように平行移動しますから、放物線 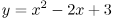 の頂点は (1, 2) です。
の頂点は (1, 2) です。
工学部 教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
|
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved. |