「 ２次関数とグラフ 」

2006.11.17 解説：教育センター　西村保三
出題：摂南大学数物系教室
工学部 教育センター ＞ SEC Video Library ＞ One-point アドバイス（数学）
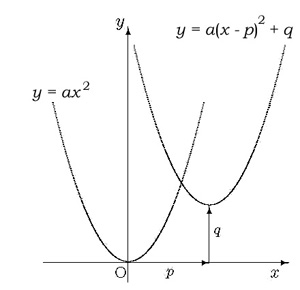
y = a ( x - p )２ + q　（ a, p, q は定数）のグラフは， y = a x２ のグラフを
x 軸の方向に p，y 軸の方向に q だけ平行移動した放物線で，
軸は直線 x = p ，頂点は点 ( p, q ) になります ．

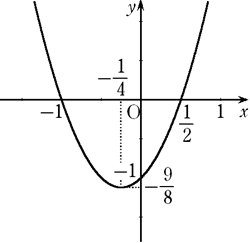
例題 ２次関数　y = 2x２ + x - 1　のグラフを描きなさい．

解　

　
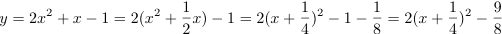
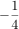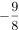より，求めるグラフは y = 2x２ を x 軸方向に ， y軸方向に だけ平行移動した 放物線．
また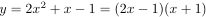　 であるから グラフは x 軸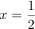と と 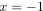の２点で交わる（図参照）．

例題　グラフが x 軸と 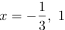で交わり， それを平行移動すると　y = 3x２ - 1　のグラフになる２次関数　y = ax２ + bx + c　を求めなさい．

解答

x 軸 と 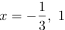で交わることから 求める2次関数の式は
　
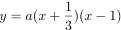
平行移動で y = 3x２ - 1 のグラフになるから a = 3． 従って求める2次関数は

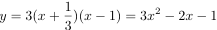
工学部 教育センタートップページへ戻る
摂南大学工学部 教育センター オリジナル教育ビデオライブラリ
Copyright © 2012-2024 Electrical and Electronic Engineering, Setsunan University, All rights reserved.
quote>